1. কোন গুণবাচক তথ্যকে পরিসংখ্যান হিসাবে গণ্য করা হয় না, এটি অবশ্যই সংখ্যাবাচক হবে।
2. পরিসংখ্যান হল একাধিক সংখ্যাগুচ্ছ, কোন একটি সংখ্যাকে পরিসংখ্যান বলা যাবে না।
3. পরিসংখ্যানের উদ্দেশ্য পূর্বনির্ধারিত।
4. পরিসংখ্যান কোন উদ্দেশ্য সাধনের জন্য উপযুক্ত তথ্য সংগৃহীত হয়ে থাকে।
5. পরিসংখ্যানে তথ্য এমনভাবে সংগৃহীত করা হয়, যাতে পরস্পরের সাথে তুলনা করা যেতে পারে।
6. পরিসংখ্যানে প্রাপ্ত তথ্যের ভিত্তিতে নতুন সিধান্ত গৃহীত হয়ে থাকে।

শিক্ষাক্ষেত্রে পরিসংখ্যানের উপযোগিতা :-

1. শিক্ষাগত তথ্যাবলির বিজ্ঞানসম্মত, সহজ, সরল ও নির্ভুল ব্যাখ্যা দানে সাহায্য করে।
2. শিক্ষাক্ষেত্রে গবেষণায় প্রাপ্ত তথ্যাবলি বিশ্লেষণের পরিসংখ্যানের যথেষ্ট উপযোগিতা রয়েছে।
3. বিদ্যালয় স্তরে মূল্যায়নের ক্ষেত্রে পরিসংখ্যানের বিশেষ উপযোগিতা রয়েছে।
4. শিক্ষামূলক ও মনোবৈজ্ঞানিক অভীক্ষার আদর্শায়িতকরণের ক্ষেত্রে পরিসংখ্যানের বিশেষ উপযোগিতা রয়েছে।
5. ছাত্র-ছাত্রীদের স্কোরের মধ্যেকার তুলনা করার ক্ষেত্রেও এর বিশেষ উপযোগিতা রয়েছে।
6. ভবিষ্যৎ ফলাফল গণনার ক্ষেত্রে পরিসংখ্যানের প্রয়োজনীয়তা রয়েছে।
7. যে কোন যুক্তিভিত্তিক সিধান্তে পৌঁছাতে, এর প্রয়োজনীয়তা রয়েছে।
8. যে কোন প্রাপ্ত তথ্যকে সুশৃঙ্খল করার ক্ষেত্রে।

পরিসংখ্যানের সীমাবদ্ধতা :-

1. উপাত্ত সঠিক নাহলে সঠিক ফলাফল পাওয়া যায় না।
2. গুনগত তথ্যের বিশ্লেষণ করা সম্ভব নয়।
3. সমষ্টিগত বিষয় ছাড়া স্বতন্ত্র বিষয়ে ধারণাদানে ব্যর্থ।
4. উদ্দেশ্যমূলক অপব্যবহার পরিসংখ্যানকে ভুল পথে চালিত করে।
5. পরিসংখ্যান দ্বারা সবসময় এক ফল পাওয়া যায় না।

পরিসংখ্যা বিভাজন

স্কোর বিন্যাসকরণের সময় একই স্কোরসম্পন্ন শিক্ষার্থীদের ফলাফল বারবার না লিখে ওই স্কোরগুলির পাশে ব্যবহৃত সংখ্যাগুলিকে লেখা। হয়, এই পুনরাবৃত্তিমূলক সংখ্যাকে পরিসংখ্যা (frequency) বলা হয়, ‘f’ চিহ্ন দ্বারা দেখানাে হয়। কিংবা সহজ ভাষায় বলতে গেলে, বিশৃঙ্খল রাশিতথ্যকে সুশৃঙ্খলভাবে সারিবদ্ধকরণ বা বিভাগীকরণকে বলে পরিসংখ্যা বিভাজন (Frequency Distribution)। এটি রাশিতথ্যকে সংক্ষিপ্ত আকারে প্রকাশ করার বৈজ্ঞানিক পদ্ধতি।

কোন বিদ্যালয়ে বার্ষিক পরীক্ষায় ছাত্রছাত্রীদের প্রাপ্ত নম্বর গুলিকে বিশ্লেষণ করলে দেখা যাবে যে, একটি বিশেষ নম্বর একজন পেয়েছে কিংবা একাধিক পেয়েছে কিংবা কেউ পায়নি। একটি স্কোরগুচ্ছের মধ্যে একটি বিশেষ স্কোর কতবার এসেছে, তার সমষ্টিকে পরিসংখ্যা বলে। যেমন- কোন শ্রেণির 50 জন ছাত্রছাত্রীর মধ্যে 15 জন 60 পেয়েছে। এখানে 60 স্কোরের পরিসংখ্যা হল 15। কোন পরিমাপ থেকে প্রাপ্ত স্কোরগুলিকে পরিসংখ্যান অনুযায়ী সাজানোকে বলা হয় পরিসংখ্যা বিভাজন।

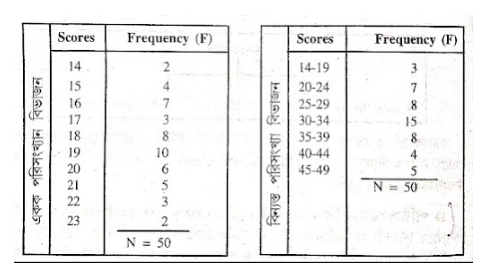
পরিসংখ্যা বিভাজনে প্রাপ্ত স্কোরগুলিকে দু’ভাবে সাজানো যায়। প্রথমত, প্রাপ্ত স্কোরগুলিকে আলাদাভাবে ছোট থেকে বড় সাজিয়ে পরিসংখ্যা বিভাজনে উপস্থাপন করা যায়, একে একক পরিসংখ্যা বিভাজন বলা যায়। আবার যখন প্রাপ্ত স্কোরগুলিকে সুবিন্যস্তভাবে শ্রেণীবদ্ধ করে পরিসংখ্যা বিভাজনে উপস্থাপন করা হয়, তখন তাকে বিন্যস্ত বা শ্রেণীবদ্ধ পরিসংখ্যা বিভাজন বলা হয়।

একটি চিত্রের মাধ্যমে দুটি বিভাজনের উদাহরণ দেখান হল-

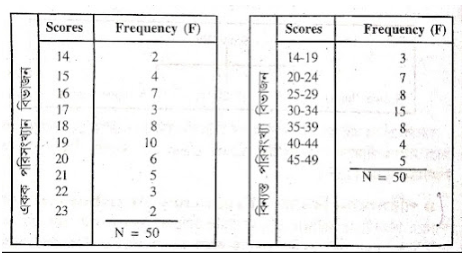
উৎস- আচার্য, অধ্যাপক পূর্ণেন্দু। শিক্ষাক্ষেত্রে মূল্যায়ন ও নির্দেশনা

পরিসংখ্যা বিভাজনের গুরুত্ব :-

 পরিসংখ্যা বিভাজনের গুরুত্ব বা প্রয়ােজনীয়তা নীচে আলােচনা করা হল—

1. স্কোরের প্রকৃতি সম্পর্কে ধারণা গঠন: যে কোনাে স্কোরের প্রকৃতি বা তার স্বরূপ সম্পর্কে ধারণা গঠন করা যায়, পরিসংখ্যা বিভাজনের ওই সংখ্যাটির অবস্থান দেখে।
2. স্বল্প পরিসরে অর্থবহ ধারণা গ্রহণ: পরিসংখ্যা বিভাজনের মাধ্যমে যে কোন স্কোরকে স্বল্প পরিসরে মধ্যে অর্থবহ করে তােলা সম্ভব।
3. তুলনামূলক আলােচনা: পরিসংখ্যা বিভাজনের মাধ্যমে দুই বা ততোধিক দলের মধ্যেকার তুলনামূলক আলােচনা করা সম্ভব।
4. ভুল-ত্রূটির সংশােধন: কোন স্কোরের মধ্যে যদি কোনাে ভুল-ত্রুটি বা অসংগতি থেকে থাকে, তবে তা পরিসংখ্যা বিভাজনের মাধ্যমে সহজেই তা দৃষ্টিগােচর হয়।
5. প্রাথমিক ধারণা গঠন: যে কোন স্কোরগুচ্ছের প্রকৃতি সম্পর্কে প্রাথমিক একটা ধারণা গঠন করতে হলে, পরিসংখ্যা বিভাজন সর্বতােভাবে সাহায্য করে থাকে।
6. লেখচিত্র অঙ্কনে: পরিসংখ্যা বিভাজনের উপর নির্ভর করেই, সকল প্রকার লেখচিত্র অঙ্কন করা হয়ে থাকে।
7. শিক্ষার্থীর উন্নতির হার পরিমাপ: কোন শ্রেণিতে উপস্থিত শিক্ষার্থীদের উন্নতির হার কীরূপ, কাদের কম বা কাদের বেশি, তা পরিসংখ্যা বিভাজনের মাধ্যমে অনুমান করা হয়ে থাকে।
8. রাশিবিজ্ঞানের বিভিন্ন কৌশল প্রয়ােগে: পরিসংখ্যা বিভাজনের সাহায্যে রাশিবিজ্ঞানের যে কোন কৌশল প্রয়ােগ (গাণিতিক ক্ষেত্রে) করতে সুবিধা হয়।

কেন্দ্রীয় প্রবণতা

According to Garrett, “Central tendency is single figure value that represents a large number of data and around which there remains the greatest amount of concentration” 

যে কোন পরিসংখ্যা বণ্টনে পরিলক্ষিত হয় যে তথ্যগুলি একটি বিশেষ বিন্দুর দিকে একত্রিত অবস্থায় অবস্থান করছে। অর্থাৎ তথ্যসারির উপরের দিকে ও নীচের দিকের তুলনায় মধ্যবর্তী স্থানে স্কোরের একত্রীকরণের প্রবণতা পরিলক্ষিত হয়। স্কোরের এরুপ প্রবণতাকে কেন্দ্রীয় প্রবণতা বলে। কেন্দ্রীয় প্রবণতার অর্থ হল কেন্দ্রের দিকে যাওয়ার ঝোঁক। একগুচ্ছ স্কোরে পৃথক মানের স্কোর থাকলে তাদের কেন্দ্রে যাওয়ার ঝোঁক বা প্রবণতা থাকে, এটাই হলো কেন্দ্রীয় প্রবণতা। অর্থাৎ এটি সমস্ত বন্টনের প্রতিনিধি রুপে কাজ করে। কেন্দ্রীয় প্রবণতা বা কেন্দ্রীয় অবস্থানের সূচক একটি বন্টনের বিভিন্ন স্কোরের মধ্যে পার্থক্য থাকা সত্ত্বেও তাদের মাঝামাঝি যাওয়ার একটি প্রবণতা থাকে।

উদাহরণস্বরূপ বলা যেতে পারে, কোন পরীক্ষা কেন্দ্রের বাইরে দাঁড়িয়ে, সেখান থেকে বাইরে আসা পরীক্ষাত্রীদের যদি জিজ্ঞেস করা হয় যে, পরীক্ষা কেমন হয়েছে? সেক্ষেত্রে অধিকাংশরাই উত্তর দেবে মোটামুটি বা মাঝামাঝি হয়েছে। আবার যে কোন পরীক্ষা পত্রের মূল্যায়ন করলে দেখা যায় যে, সেখানে মধ্যবর্তী স্থানে প্রাপ্ত নম্বরের সংখ্যা বেশি থাকে। বিভিন্ন স্কোরগুচ্ছের মাঝামাঝি স্থানে যাওয়ার যে প্রবণতা, তাকেই বলে কেন্দ্রীয় প্রবণতা।

According to Hans Raj, “Central Tendency is a device to know the position of different groups.”

কেন্দ্রীয় প্রবণতার পরিমাপ :-

কেন্দ্রীয় প্রবণতার তিনটি পরিমাপ হল, যথা- মিন (Mean), মিডিয়ান (Median) ও মোড (Mode)। এদের ব্যবহার সম্পর্কে নিচে আলোচনা করা হলো –

1. কেন্দ্রীয় প্রবণতার সবচেয়ে নির্ভরযোগ্য পরিমাপ জানার প্রয়োজন হলে, তখন গড় (Mean) ব্যবহার করা হয়ে থাকে।
2. যখন কোন রাশিমালার ব্যাপক তাৎপর্য নির্ণয়ের প্রয়োজন হয়, তখন গড় (Mean) ব্যবহার করা হয়।
3. রাশিবিজ্ঞানের অন্যান্য পদ্ধতি প্রয়োগের ক্ষেত্রে প্রয়োজন হয়। যেমন- আদর্শ বিচ্যুতি নির্ণয় করার সময় গড়ের প্রয়োজন হয়।
4. যে কোন রাশিমালার বিভিন্ন স্কোরের মধ্যে বৈশিষ্ট্যমূলক তুলনার ক্ষেত্রে গড়ের ব্যবহার করা হয়।
5. কেন্দ্রীয় প্রবণতার একটি সহজ ও সরল পদ্ধতি হিসাবে গড়-কে বেছে নেওয়া হয়।

মধ্যমানের ব্যবহার :-

1. যে কোন রাশিমালায় দ্রুত কেন্দ্রীয় প্রবণতার মান জানার প্রয়োজন হলে, সেক্ষেত্রে মধ্যমানের ব্যবহার করা হয়ে থাকে।
2. রাশিমালার বন্টনের মধ্যবিন্দু জানার প্রয়োজন হলে মধ্যমানের ব্যবহার করা হয়।
3. যখন পরিসংখ্যা বিভাজন বেশি মাত্রায় স্কুড থাকে তখন মধ্যমানের ব্যবহার করা হয়।
4. কোন একটি রাশিমালার বন্টনে যদি কোন প্রকার অসমতা থাকে, তাও সেক্ষেত্রে মধ্যমানের ব্যবহার করা হয়ে থাকে।
5. কোন রাশিমালাকে সমান দুটি ভাগে ভাগ করতে গেলে, সেক্ষেত্রেও মধ্যমানের ব্যবহার হয়।

1. যখন কেন্দ্রীয় প্রবণতার মান দ্রুত জানার প্রয়োজন হয়, তখন মোডের ব্যবহার করা হয়।
2. যে কোন গাণিতিক গণনা ছাড়া, যদি কেন্দ্রীয় প্রবণতার সম্বন্ধে ধারণা পেতে মোডের প্রয়োজন হয়।
3. কোন বন্টনে অধিকবার কোন সংখ্যাটির পুনরাবৃত্তি ঘটেছে, তা জানতে মোড ব্যবহার করা হয়ে থাকে।

 সহায়ক গ্রন্থপঞ্জি

1. আচার্য, অধ্যাপক পূর্ণেন্দু। শিক্ষাক্ষেত্রে মূল্যায়ন ও নির্দেশনা। শ্রীতারা প্রকাশনী, পৃষ্ঠা : ৬১-৮৫
2. চক্রবর্তী, ড. অনিরুদ্ধ। শিক্ষায় পরিমাপ ও মূল্যায়ন। ক্লাসিক বুকস্, পৃষ্ঠা : ১৫৮-২০৬
3. ইসলাম, ড. নূরুল। শিক্ষায় মূল্যায়ন ও পরিমাপ। শ্রীধর প্রকাশনী, পৃষ্ঠা : ১৪১-১৭৮
4. রহমান, মোঃ লুৎফুর., খান, এ. কে. এম. শওকত আলী., দাস, স্বপন কুমার। গবেষণা পদ্ধতি ও পরিসংখ্যান। গ্রন্থ কুটির, ঢাকা, পৃষ্ঠা : ৪-২০

_________________________________