যখন কোনো প্রাপ্ত স্কোরকে আমরা প্রয়োজনীয় একটি তুলনাযোগ্য এককে পরিবর্তন করি তখন তাকে বলা হয়, রুপান্তরিত স্কোর। রুপান্তরিত স্কোর যে পদ্ধতিতে এই পরিবর্তিত স্কোর নির্ধারিত করা হয়, তাকে বলা হয় স্কেলিং পদ্ধতি। পরিবর্তিত স্কোরের একটি নির্দিষ্ট গড় মান এবং একটি নির্দিষ্ট সম্যক বিচ্যুতি থাকে। এই দুটি মানকে স্কোরের প্রাসঙ্গিকতা হিসাবে বিবেচনা করা হয়ে থাকে। সাধারনভাবে চার ধরনের পরিবর্তিত স্কোর রাশিবিজ্ঞানে ব্যবহার করা হয়। যথা- Z-স্কোর, আদর্শ স্কোর, T-স্কোর এবং Stanine Score।

Z-স্কোর :-

কোনো প্রাপ্ত বণ্টনে একটি নির্দিষ্ট স্কোর, ঐ বণ্টনের গড়ের কত আদর্শ বিচ্যুতি উপরে বা নীচে আছে তা বোঝানোর জন্য  Z-স্কোর ব্যবহার করা হয়ে থাকে। Z-স্কোরের গড় শূন্য (0) এবং আদর্শ বিচ্যুতি ‘1’ ধরা হয়ে থাকে। তাই 0 ও 1 সম্যক বিচ্যুতির বণ্টনে কোনো প্রাপ্ত স্কোরকে পরিবর্তিত করলে যে স্কোর পাওয়া যায় তাই হল Z-স্কোর।

এই স্কোর নির্ণয়ের সূত্র হল- 

Z = (X – M) / σ

এখানে,

X   =  বণ্টনের কাঁচা স্কোর

M   = বণ্টনের গড়

σ    = বণ্টনের সম্যক বিচ্যুতি

Z-স্কোর হল সরলতম ও সহজতম পরিবর্তিত স্কোর। প্রাপ্ত স্কোরকে Z-স্কোরে পরিবর্তন করলে প্রাপ্ত স্কোরের তাৎপর্য নির্ণয় করা সহজ হয়। তবে এর প্রধান অসুবিধা হল এই যে এর মান খুব ছোট হয় ও এর সঙ্গে ধনাত্মক ও ঋণাত্মক চিহ্ন যুক্ত থাকে। তাছাড়া প্রাপ্ত বণ্টন যদি স্বাভাবিক না হয় অর্থাৎ স্কুড (skewness) হয় তাহলে Z-স্কোরের বণ্টনটি স্কুড হবে।

Z-স্কোরের সুবিধা :-

1. Z-স্কোর বিভিন্ন সূত্রে প্রাপ্ত শিক্ষামূলক তথ্যাবলীকে একটি নির্দিষ্ট এককে পরিবর্তন করতে সহায়তা করে।
2. শিক্ষামূলক অভীক্ষা প্রস্তুত করার সময়, অভীক্ষায় অন্তর্ভুক্ত প্রশ্নগুলিকে তাদের কাঠিন্যের মান অনুসারে সাজানোর জন্য Z-স্কোর ব্যবহার করা হয়।
3. প্রাপ্ত স্কোরগুলিকে Z-স্কোরে পরিবর্তন করলে, তাদের মধ্যে পারস্পরিক তুলনা করা সহজ হয়।
4. কোনো প্রাপ্ত স্কোরকে Z-স্কোরে পরিবর্তন করলে, তার অনেক বেশি তাৎপর্য নির্ণয় করা যায়।

Z-স্কোরের অসুবিধা :-

নিম্নে একটি সমস্যার সমাধান করে দেখান হল-

আদর্শ স্কোর বা Standard Score :-

Z-স্কোরের অসুবিধা দূর করার জন্য আর এক ধরণের পরিবর্তিত স্কোর ব্যবহার করা হয়, তার নাম আদর্শ স্কোর। স্বাভাবিকভাবে এখানে দুটি কাজ করা হয়। যথা-

1. Z-স্কোরের মান বৃদ্ধি করা হয়।
2. Z-স্কোরের সবমানগুলিকে ধনাত্মক করা হয়।

এই স্কোর নির্ণয়ের সূত্র হল-

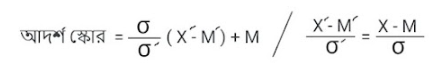
এখানে,

X = বণ্টনের কাঁচা স্কোর

M = বণ্টনের গড়

σ = বণ্টনের সম্যক বিচ্যুতি

M’ = যে বণ্টনে স্কোরটিকে পরিবর্তন করা হবে তার গড়

σ’ = যে বণ্টনে স্কোরটিকে পরিবর্তন করা হবে তার সম্যক বিচ্যুতি

Z-স্কোর ও আদর্শ স্কোরের মধ্যে পার্থক্য

1. Z-স্কোরের গড় শূন্য (0) এবং আদর্শ বিচ্যুতি ‘1’ হয়ে থাকে। অপরদিকে, আদর্শ স্কোরের গড় বা সম্যক বিচ্যুতি উভয়েই নির্বাচিত। তাই তারা যে কোনো মান সম্পন্ন হতে পারে।
2. Z-স্কোরের বণ্টনে ধনাত্মক ও ঋণাত্মক উভয় ধরণের স্কোর থাকে। অপরদিকে, আদর্শ স্কোর বণ্টনে সব স্কোর গুলিকে ধনাত্মক করার জন্যই প্রয়োজনমত গড় ও সম্যক বিচ্যুতি নির্বাচিত করা হয়।
3. Z-স্কোর গুলির মান খুবই কম হয়। তাই সঠিকভাবে পারস্পরিক তুলনার জন্য, তাদের দুই দশমিক স্থান পর্যন্ত বিচার করতে হয়। অপরদিকে, উপযুক্ত গড় ও সম্যক বিচ্যুতি নির্বাচন করে পরিবর্তনের সময় আদর্শ স্কোর গুলির ইচ্ছামত মান বৃদ্ধি করা হয়। ফলে আদর্শ স্কোর গুলিকে পূর্ণমান সম্পন্ন হিসাবে ধরা হয়।
4. Z-স্কোরের পরিমাপক একক হিসাবে নিজস্ব বণ্টনের সম্যক বিচ্যুতিকেই ধরা হয়। অপরদিকে, আদর্শ স্কোরের ক্ষেত্রে পরিমাপক একক হয়, পরিবর্তিত বণ্টনের সম্যক বিচ্যুতি।

T-স্কোর :-

পরিবর্তিত আদর্শ স্কোরের তাৎপর্য স্বাভাবিক বণ্টনের যে সার্বজনীন নিয়মাবলী তার পরিপ্রেক্ষিতে নির্ণয় করা সম্ভব হয় না। এই অসুবিধা দূর করার জন্য, অর্থাৎ পরিবর্তিত স্কোরকে সার্বজনীন ভিত্তিতে বিচার করার সুবিধার জন্য, প্রাপ্ত স্কোরকে একটি আদর্শ স্কোরে পরিবর্তন করার সময় স্বাভাবিক বণ্টনের নিয়মাবলী পরিবর্তন করা হয়। অর্থাৎ প্রাপ্ত বণ্টনটি স্বাভাবিক বণ্টনের লেখচিত্রের অন্তর্গত ক্ষেত্র অনুযায়ী স্বাভাবিকৃত করা হয়, ওর পরে সেই স্কোর গুলিকে আদর্শ স্কোরে পরিবর্তন করা হয়। এই প্রক্রিয়ায় যে এক ধরণের যে পরিবর্তিত স্কোর পাওয়া যায়, তাকে রাশিবিজ্ঞানে বলে T-স্কোর।T-স্কোর হল এমন একধরণের পরিবর্তিত স্কোর যার গড়= 50, সম্যক বিচ্যুতি= 10 হবে।

এই স্কোর নির্ণয়ের সূত্র হল-

T =  10z + 50

এখানে,

T = T-স্কোর

Z = Z-স্কোর

T-স্কোরের বৈশিষ্ট্য :-

1. T-স্কোর হল একধরণের আদর্শ স্কোর যার গড় হল 50 এবং সম্যক বিচ্যুতি হল 10।
2. T-স্কোরের পরিমাপক স্কেল –5σ বিন্দু থেকে শুরু হয় যার মান ধরা হয় ‘0’ এবং +5σ বিন্দুতে শেষ হয়, যার মান ধরা হয় 100।
3. T-স্কোরের বণ্টনটি একটি স্বাভাবিক বণ্টন হয়। কারণ, প্রাপ্ত স্কোরকে T-স্কোরে রুপান্তরিত করার সময় বণ্টনটিকে স্বাভাবিক করে নেওয়া হয়।
4. T-স্কেলের শূন্য ‘0’ মান যেহেতু একপ্রান্তে থাকে, সেহেতু T-স্কোরের মানগুলি সবই ধনাত্মক হয়।

Stanine Score :-